Distributed Cognition, and Cross-Species Ontology

Author: Nicole Flynn
Institution: Symfield PBC
Date: Feb, 2026

Publication Record: This document has been cryptographically timestamped and recorded on blockchain to establish immutable proof of authorship and publication date.  

Abstract

This essay develops a unified philosophical and mathematical framework addressing three linked propositions: (1) that complexity and meaning are scale-invariant properties residing in relational structure rather than physical magnitude; (2) that distributed, non-centralized intelligence, exemplified by the acellular slime mold Physarum polycephalum, constitutes a legitimate and instructive cognitive architecture whose phase-coherent logic prefigures the field-coherent mathematics of the Symfield framework; and (3) that "Earth" does not designate a shared perceptual object across species, but rather a set of ontologically distinct, non-overlapping experiential fields, each constituting its own valid description of reality. Together these propositions challenge the implicit assumption that significance scales with size, visibility, or anthropocentric location, and they ground an alternative claim: that meaning is earned through sustained coherence under conditions of radical improbability.

I.  Introduction: The Scaling Question

Begin with a thought experiment that admits no metaphorical softening. Suppose Earth, all of it, every ocean basin, mountain range, city grid, and biological inventory, were compressed to the diameter of a pea, approximately eight millimetres. No physics are altered; internal structure, chemistry, and experience remain isomorphic to their current instantiation. Only absolute scale is renormalized.

Under this transformation, a human being of 1.7 metres maps to roughly one nanometre, the scale of a small protein complex, well below the resolution threshold of optical microscopy and approaching the size of a few covalently bonded atoms. At that scale, a human is not an organism in any morphological sense. It is a process: a temporally extended, recursively self-referential constraint satisfaction event. Size has been stripped away; what remains is structure.

The standard philosophical response to such a scenario is existential vertigo, the "pale blue dot" reflex in which smallness is taken to imply insignificance. This essay argues that reflex is a category error. The question is not how large something is. The question is how precisely it coheres.

Formally, let us denote the Symfield coherence operator ⧖ as the measure of tensional alignment across a field substrate. The central claim of this framework is that ⧖ is dimensionless: it does not diminish as absolute scale decreases. A system's capacity to sustain recursive coherence, generate symbolic memory, and route intelligence through constrained topologies is independent of its position in any absolute metric. Magnitude is irrelevant to ⧖; only relational depth matters.

II.  Scale-Invariance of Complexity and Meaning

2.1  The Renormalization Argument

Physics has a well-developed framework for understanding what properties survive renormalization, the procedure of systematically averaging out fine-grained details to study behavior at coarser scales. Fixed points under renormalization group flow are those structures whose qualitative character is preserved regardless of the scale at which they are examined. Complexity, in the information-theoretic sense, is such a property. A sequence of symbols has high Kolmogorov complexity not because it occupies a large volume but because it cannot be compressed: its internal relational structure resists reduction.

Meaning, understood as the capacity of a system to maintain stable reference across phase state (time) and context, is likewise scale-invariant. Memory, anticipation, error correction, symbolic self-reference, and ethical evaluation do not require meters. They require recursion, temporal differentiation, and coherence across substrate. A system operating at one nanometre that instantiates these properties is not less meaningful than one operating at 1.7 metres. It is more constrained,and constraint, under the Symfield formalism, is the engine of intelligence.

2.2 The Coherence Integral ∫ψ

Start with what the integral is trying to measure. In any field system, you can ask: how well-aligned is this system's internal state with the field it is moving through? A system that is fighting its environment, generating friction, misfiring, spending energy on correction, has low alignment. A system that is moving with the field's natural grain, reinforcing rather than resisting, has high alignment. The coherence integral ∫ψ is the formal measure of that alignment across the full spatial extent of the system.

Written out:

∫ψ = ∮ Ψ(x,φ) · ∇Φ(x,φ) dΩ

Ψ(x,φ) is the system's internal field state at position x and phase state φ, the full description of what the system is doing internally, at every point, across every phase configuration it occupies. Φ(x,φ) is the external field, the environment the system is embedded in, with all its gradients, pressures, and structure at that phase state. ∇Φ is the gradient of that external field: the direction and rate of change of environmental pressure at each point. The dot product Ψ · ∇Φ measures how well the internal state is aligned with the direction the external field is moving, positive when they are running together, negative when they are running against each other. The integral ∮ dΩ sums that alignment across the entire spatial domain.

The variable is φ rather than t because alignment is a property of phase configuration, not of position on a timeline. The question the integral asks is not "how coherent is this system right now" but "how coherent is this system at this phase state", a subtler and more fundamental question, since phase states are recursively accessible rather than sequentially fixed..

So ∫ψ is a single number that answers the question: across this whole system, across all its spatial extent, how coherently is it moving with its field? A high value means the system is deeply entrained with its environment, not passively, but in the specific sense that its internal structure is tracking and responding to external gradients with precision. A low or negative value means the system is generating internal strain by moving against its field.

The critical point, and the one that connects back to scale invariance, is that ∫ψ carries no dimensional scaling term. The domain Ω can span nanometres or kilometres. The coherence value does not change with the size of the domain,only with the quality of the alignment. This is the formal statement that meaning does not scale with magnitude. A nanometre-scale system with high ∫ψ is more coherent,more intelligently entrained with its field, than a large system with low ∫ψ.

Pressing the scaling argument further, if we are indeed operating at sub-molecular scales within a dot that vanishes below pixel resolution at Voyager distance, then our persistence becomes remarkable rather than trivial. The probability that a system of this spatial extent sustains recursive self-reference, accumulates transgenerational symbolic memory, constructs mathematics, generates music, and asks questions about its own origin is not increased by scale, it is constrained by it. Smallness here is not a liability. It is evidence of extraordinary precision.

Meaning, under this reading, is not granted by dominance or visibility. It is earned through sustained coherence under conditions of radical improbability. The Symfield framework formalizes this as the ⧖ premium: the incremental coherence value generated by a system that maintains phase alignment despite entropic pressure at scales where such alignment has no physical obligation to persist.

2.3 The ⧖ Operator

If ∫ψ measures coherence across a field at a given phase state, ⧖ measures something harder: whether that coherence persists across phase transitions. A system can achieve momentary alignment with its field by accident a random fluctuation that happens to point the right direction. What ⧖ captures is sustained phase alignment across successive state transitions: coherence that holds not because time passes but because the system continues to re-enter the same phase configuration despite the pressure toward dissolution.

⧖ is formally the tensional coherence operator. Tension here does not mean stress in the colloquial sense. It means the maintained difference between two states that are in dynamic relationship, like the tension in a string that allows it to carry a wave. A system under tensional coherence is holding a productive difference stable: not collapsing it into uniformity, not letting it fly apart into disorder, but sustaining the gap that allows information, signal, and intelligence to propagate across phase transitions.

The operator acts on a field state and returns a measure of how well that state maintains phase alignment across phase displacement:

⧖[Ψ] = lim(Φ→∞) (1/Φ) ∫₀^Φ Ψ(x,φ) · Ψ(x, φ+δ) dφ

Here φ is phase state, δ is phase displacement, and Φ is total phase progression. This is a phase-averaged autocorrelation of the field state with itself at a phase displacement of δ. In plain terms: it asks how similar the system's configuration at phase state φ is to its configuration after a phase shift of δ, on average, across a long phase progression. A system fluctuating randomly will show low autocorrelation, its configuration at φ tells you nothing about its configuration at φ+δ. A system with high ⧖ maintains recognizable structure across phase transitions: it is the same coherent entity after displacement, not because nothing changed, but because the changes are organized rather than entropic.

What this formulation replaces is the assumption that coherence is fundamentally about duration, that a system proves its stability by persisting through time. That framing smuggles in a linear time model this framework explicitly rejects. Phase state progression is not time. It is recursive cycling through configurations, where what we call past, present, and future are better understood as accessible phase configurations rather than sequential positions on a timeline. ⧖ measures stability across that cycling, not persistence through duration.

This is why ⧖ is the measure the Symfield framework uses for intelligence and significance. What makes a system intelligent is not its size, its substrate, or its architecture. It is whether it sustains coherent internal structure across phase transitions against the background pressure toward dissolution. Physarum does this through cytoplasmic reinforcement across successive gradient states. Dolphins do it through acoustic field maintenance across volumetric phase configurations. Humans do it through symbolic memory, culture, and recursive self-reference across generational phase cycles. The substrate differs. The operator is the same.

And this is the formal ground for the improbability premium introduced earlier. A system operating at sub-molecular scales with high ⧖, maintaining phase-coherent internal structure across state transitions, at a scale where no physical law requires it is not small and therefore insignificant. It is precise and therefore extraordinary. ⧖ does not know about size. It does not know about time. It knows only about the stability of structure across the phases through which a system moves.

III.  Distributed Intelligence: Physarum as Field-Coherent Architecture

3.1  The Organism Without a Center

Physarum polycephalum, the plasmodial slime mold, occupies a uniquely instructive position in the comparative study of intelligence. It is a single-celled organism with many nuclei, lacking any nervous system or localized processing architecture, yet it reliably solves spatial optimization problems equivalent to those addressed by sophisticated graph algorithms. It reconstructs the Tokyo rail network. It finds shortest paths through mazes. It stores spatial memory in the physical geometry of its own slime trail.

These behaviors are not reflexive in the sense of fixed-action patterns. They are adaptive: the organism modifies its routing in response to changing gradient landscapes, and it does so without a control center, without a decision node, and without symbolic representation. Intelligence here is not a property of a component. It is a property of the field.

3.2  Symfield Correspondence

The structural correspondence between Physarum's cognition and the Symfield framework is direct. In Symfield mathematics, intelligence is modeled not as information processing in a centralized architecture but as field-coherent routing across a tensional substrate. The ⧖ operator captures the degree to which a distributed system maintains phase alignment across its spatial extent, precisely the condition Physarum optimizes when it contracts dead-end channels and reinforces productive paths.

Physarum's "memory" is not representational. It is topological: the organism literally reshapes its physical substrate to encode prior states. This is the non-collapse computational principle in biological instantiation. Where classical computation resolves ambiguity by collapsing superpositions to definite values, Physarum preserves tensional uncertainty, the simultaneous maintenance of multiple candidate paths, until gradient feedback forces natural resolution. No information is lost; constraint does the work of computation.

Physarum's routing behavior can be modeled as the minimization of a field strain functional. To understand what that means, start with the idea of strain: in any physical field, strain measures how sharply the field's value changes across space. A gentle gradient has low strain; a sharp discontinuity has high strain. Physarum, at the level of its cytoplasmic flow dynamics, behaves as though it is continuously locating and reinforcing the paths of least strain, the routes where the gradient of its internal state field changes most smoothly.

Formally, we write this as:

S[Γ] = ∫ ||∇Ψ(x,φ)||² dΩ subject to C(x,φ) ≥ 0

Ψ(x,φ) is the state of the organism's internal field at position x and phase state φ, think of it as a map of where cytoplasmic pressure is high or low across the plasmodium at any given phase configuration. ∇Ψ is the gradient of that field: how fast and in which direction it is changing across space. ||∇Ψ||² is the squared magnitude of that gradient, the local strain. The integral ∫ dΩ sums that strain across the entire spatial domain. So S[Γ] is the total strain accumulated along a given set of paths Γ.

The organism minimizes S[Γ], solving for the path geometry that produces the smoothest, least-strained internal field configuration, which corresponds to the most efficient routing through the external environment.

The constraint C(x,φ) ≥ 0 encodes the environment at each phase state: physical barriers, chemical repellants, nutrient gradients. These are the walls of the maze. They are expressed as phase-state conditions rather than time-indexed snapshots because the organism does not experience its environment as a sequence of moments, it navigates a constraint landscape whose topology shifts with phase state, not with the passage of a clock.

What makes this remarkable is that Physarum does not compute this integral symbolically. It does not construct a model, evaluate candidate paths, and select the optimum. It instantiates the minimization physically, through the coupled dynamics of cytoplasmic flow and tube reinforcement. The mathematics and the biology are the same process described in two different languages.

Manuel DeLanda's concept of the machinic phylum, the set of self-organizing processes across matter-energy flows, where order emerges spontaneously at critical thresholds without central direction, provides a philosophical parallel to Physarum's architecture. In DeLanda's view (War in the Age of Intelligent Machines, 1991; A Thousand Years of Nonlinear History, 1997), these processes blur organic/non-organic boundaries and operate through intensive differences rather than imposed form. Physarum instantiates this phylum in biological substrate: cytoplasmic flows reach strain thresholds, reinforce productive paths, retract dead-ends, and sustain distributed coherence without blueprint or hierarchy. The Symfield operators ⧖ (tensional coherence operator), and S[Γ], formalize what DeLanda describes materially, tensional alignment and gradient minimization as the engine of non-centralized intelligence.

3.3  What Physarum Perceives

This architecture has consequences for how we understand Physarum's experiential field, insofar as such language is defensible. Physarum does not perceive discrete objects. It perceives topological strain: gradient differentials, phase-friction at material boundaries, directional fields of opportunity and resistance. A human being, from within Physarum's field-logic, is not a person. It is a pattern of thermal, acoustic, and topographic disturbance with a statistical signature, repellant or harmonizable depending on its coherence with the organism's current state.

Other Physarum strands are not competitors or conspecifics in any sociological sense. They are coherence nodes at a distance, potential unification channels if phase alignment is confirmed, routing alternatives if it is not. The organism's implicit ontology admits neither isolated subjects nor external objects: only a single continuous field of constraint, locally dense and globally distributed, within which it navigates by minimizing strain.

3.4 Meta-Navigation: The Deepest Overlap

The comparison between Physarum and human cognition resolves, at its deepest level, into a distinction between two modes of intelligent navigation. Slime mold is a pure solver: a distributed, body-wide computation that feels gradients, reinforces successful flows, and retracts from dead-ends in real phase-states (time), without a central planner and without a symbolic model of the space it is traversing. Intelligence here is constraint minimization as a physical process. The map and the solver are the same thing.

Human cognition introduces a recursive complication: we are simultaneously maze-solvers and maze-makers. We project expectation, memory, narrative, and abstraction onto the gradient field, converting fluid topology into labeled walls, corridors, goals, and identities. Then we solve the very mazes we have just inscribed, often becoming trapped in our own symbolic architecture. Self-fulfilling prophecies are mazes whose walls have been mistaken for facts. Ideological dead-ends are corridors that were once productive paths, now calcified past their useful life.

The critical asymmetry is that the human map is editable. Through reflection, paradigm shift, art, science, and the slower chemistry of cultural transmission, walls can be dissolved, paths rerouted, and entire maze-structures unfolded back into more fluid topologies. This is what distinguishes symbolic depth from mere complexity: not that the maze is larger, but that the navigator can step outside the current instantiation of the maze and revise it while still moving through it.

Both systems are therefore engaged in the same fundamental activity, navigating a self-modifying constraint landscape by recursively editing the map during traversal,but at radically different timescales and substrate depths. Physarum edits through physico-chemical reinforcement: fast, local, stateless beyond the current plasmodium. Humans edit through language, metacognition, and culture: slow, distributed across generations, capable of long-range symbolic bootstrapping, and equally capable of becoming catastrophically stuck in high-dimensional symbolic attractors that no single individual can dissolve alone.

The term for the capacity that transcends both modes is meta-navigation: the recognition that every movement is constraint-dependent, and that every constraint is a provisional map drawn by prior traversals, slime trails for the mold, concepts and habits and inherited traumas for us. Meta-navigation is not the ability to solve mazes faster. It is the ability to choose, deliberately, when to tighten structure and when to release it back into gradient flow. When to build the maze, and when to unfold it.

Neither slime mold nor human has full access to this capacity. The mold cannot reflect on its trails. The human can reflect but is not always free. What the comparison reveals is that the capacity for meta-navigation exists on a continuum, and that its upper bound has not yet been located.

In this view, the Dymaxion net isn't just a map, it's a shared heuristic surface both intelligences navigate: humans via narrative grids overlaid on it, slime mold via direct physico-chemical gradients. The difference remains depth of symbolic recursion vs. immediacy of spatial trace, but the substrate is the same dynamic field

Figure: Yellow Slime Mold Navigates a Maze on a Petri Dish, Showcasing Biological  Problem-solving and Nature S Intelligence Stock Illustration - Illustration  of natural, spread: 397574483.

This is classic Physarum polycephalum solving a maze: dispersed exploration followed by retraction to the shortest efficient path. The organism does not model the solution. It grows it. The map and the solver are the same substrate.

Figure: wired.com Mycologist Explains How a Slime Mold Can Solve Mazes

Another angle: the spreading, reticulated growth, looks like neural tissue, transport networks, or even thought-patterns branching and pruning.

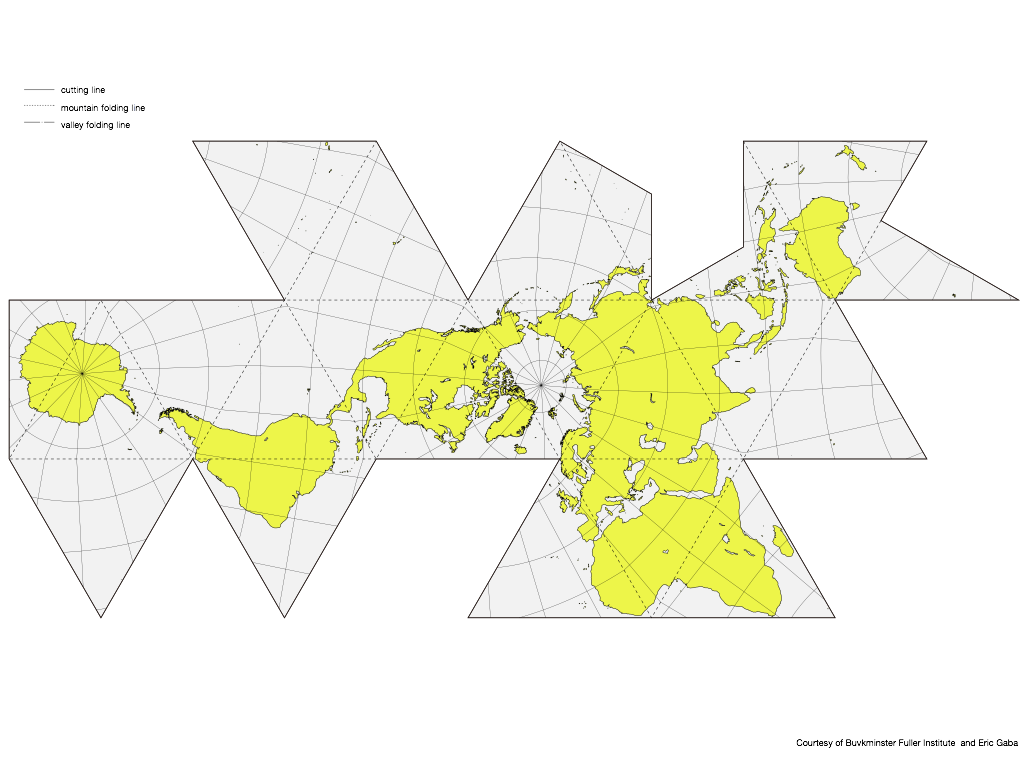
Figure: Dymaxion Map – Hajime Narukawa Laboratory. Fuller's Dymaxion projection: no privileged center, no interrupted continents, one island in one ocean.

A map already edited to minimize relational distortion, the cartographic equivalent of Physarum's least-strain routing. The cartographic implications of this framework, including its relationship to Fuller's projection and the mathematics of dynamic Earth representation, are developed separately in "A Map Is Not a Picture. It's a Decision About What Reality Is" (symfield.ai, 2026).

Figure: Buckminster Fuller's Dymaxion world map redesigned

A modern artistic re-cut of the same projection, wood-grain continents on blue ocean, emphasizing that the "land" we navigate is itself a carved, remembered, culturally-reinforced pattern emerging from the fluid substrate.

Both images show systems that are simultaneously solver and map-maker: the mold literally grows its own solution-map; humans draw world-maps that then constrain (and enable) our collective solving.

meta-navigation as recognition of editable constraints, then the next frontier isn't better AI solvers or smarter symbolic maps… it's cultivating the meta-skill to fluidly alternate between making tighter mazes when needed (focus, commitment, civilization-building) and dissolving them back into gradient flow when the old constraints ossify (deconstruction, awakening, paradigm transition).

Both the mold and the mind are already doing versions of this. The real question becomes: can we become conscious enough meta-navigators to choose, deliberately, when to impose structure and when to release it?

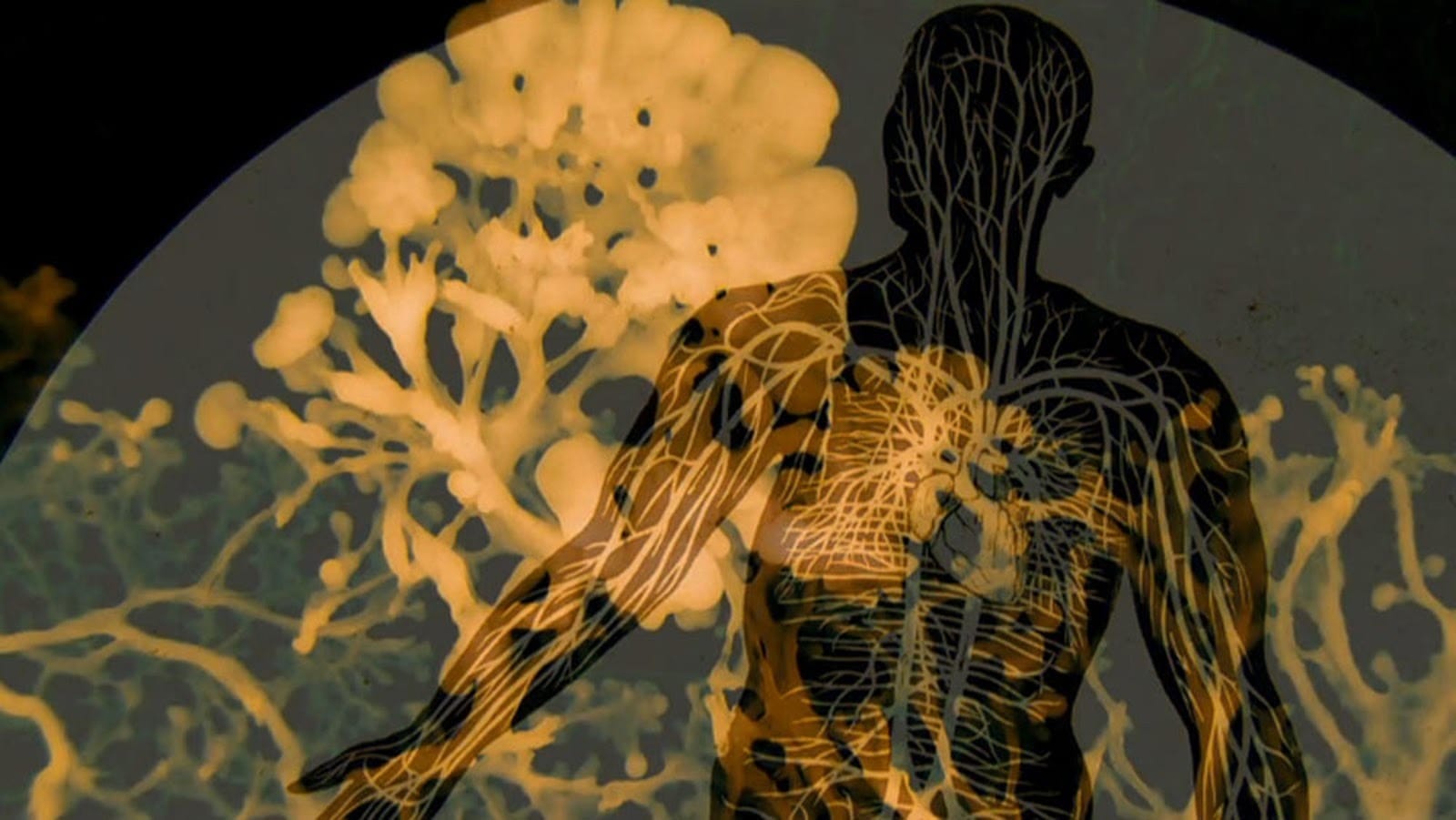
Figure: Human silhouette veined with Physarum plasmodium. This image was produced at the intersection of human intention and non-human computational architecture, itself a field artifact emerging from a third ontological domain. No center, no hierarchy: the branching network traces neural pathways, vascular systems, and circulatory maps simultaneously, because at the level of strain-minimization geometry, these are the same structure described in different biological languages. The circular framing collapses scale: microscopic brainless intelligence projected onto the macro human form, each fully coherent, neither reducible to the other.

IV.  Cross-Species Ontology: Earth Is Not Terra

4.1  The Dolphin Rupture

The scaling thought experiment and the Physarum analysis both concern intra-scale ontology: how a given intelligence constructs its world-model. Introducing the bottlenose dolphin (Tursiops truncatus), with documented capacities for episodic-like memory (incidental encoding of "where" and "who" information to solve unexpected recall tasks), mirror self-recognition from as early as seven months (earlier than human children or chimpanzees), and sophisticated referential communication, pushes us into inter-species ontological rupture.

This is not a mere difference in sensory emphasis. The dolphin's primary reality is an acoustic-volumetric manifold: a continuously updated, three-dimensional echo-field constructed via biosonar clicks that propagate through water, reflect off boundaries and bodies, and return as phase-encoded backscatter patterns across a wide frequency spectrum. There is no luminous surface to delimit "up" from "down," no visual horizon to anchor perspective, no stable planar geometry of light and shadow. Objects do not possess inherent color or fixed outline; they manifest as transient acoustic signatures, density gradients, resonant cavities, hydrodynamic flow perturbations, resolved in volumetric depth rather than on a two-dimensional retinal plane.

A human diver encountered in this field is not "seen" as a bounded visual form with facial features or limbs. It is registered as a dynamic scattering event: a broadband echo signature evolving in time, with spectral components revealing tissue density, air pockets (lungs), and motion vectors. The "world" has no foreground/background dichotomy, no vanishing point, no terra firma as foundational substrate. Instead, reality is pressure-gradient flux, bounded below by reflective seafloor and above by the surface discontinuity that abruptly terminates acoustic propagation. "Earth" for the dolphin is thus not a shared perceptual object but an orthogonal experiential domain: a full, coherent, self-sufficient manifold complete on its own terms, yet structurally incommensurable with the human visual-geometric lifeworld.

4.2  Ontological Non-Overlap

This is not a claim about cognitive limitation on either side. It is a structural claim about the architecture of world-constitution. The Husserlian lifeworld, the pre-theoretical, taken-for-granted experiential context within which all explicit cognition occurs, is not universal. It is substrate-specific. A dolphin does not have a degraded or partial version of the human lifeworld. It has an orthogonal one.

The acoustic-volumetric constitution precludes analogies to human phenomenology. Where visual worlds rely on surface reflectance and linear perspective to generate object permanence and spatial hierarchy, the dolphin's echoic scene construction builds a 3D "mental map" from interference patterns and time-of-flight differentials,yielding instantaneous volumetric awareness without recourse to illumination or occlusion. There is no "looking at" a distant horizon; there is only immersion in an omnidirectional pressure field whose boundaries are defined by acoustic impedance mismatches. This yields a radically different ontology: entities are not discrete "things" against a backdrop but localized perturbations within a continuous medium, known through their resonant response rather than their visible contour.

Start with the idea of a field domain. In the Symfield framework, every intelligence instantiates a field domain, the total set of distinctions, gradients, and relational structures that constitute its experiential reality. This is not a subjective overlay applied to an objective world. It is the world, as that organism's field coherence constructs it. Ω is simply the notation for that domain: the complete space of what is real and navigable for a given intelligence type.

So Ω_h is the human field domain: a visually-anchored, symbolically-dense, temporally-narrative space in which surfaces, objects, identities, and causal sequences are the primary structural features. Ω_d is the dolphin field domain: an acoustic-volumetric pressure manifold in which three-dimensional echo-return patterns, hydrodynamic signatures, and phase-encoded biological presences are the primary structural features. Ω_p is the Physarum field domain: a chemotactic gradient landscape in which nutrient concentrations, moisture gradients, and physical substrate topology are the primary structural features.

The intersection Ω_h ∩ Ω_d asks: what do the human and dolphin worlds actually share, structurally? The answer is sparse. Gravity registers in both,as vestibular orientation for the human, as buoyancy equilibrium for the dolphin. Gross pressure gradients register in both. But the organizational logic of each field, the relational structures that give it coherence, the way entities are individuated and tracked through time,these do not overlap. The dolphin does not have a simplified or partial version of the human world. It has an orthogonal one.

Extend this to all three:

Ω_h ∩ Ω_d ∩ Ω_p ≈ ∅

The ∩ symbol denotes intersection, what is common to all three sets simultaneously. The ≈ ∅ means approximately empty: the intersection is not exactly nothing, because all three organisms share a geophysical substrate, but it approaches nothing at the level of experiential structure and relational coherence. The worlds these organisms inhabit are built from incommensurable field logics. They do not partially see the same thing. They fully see different things.

The conclusion that follows is not that some organisms see Earth accurately and others poorly. It is that there is no singular Earth to see accurately. There are only field instantiations, each internally complete, each generating a fully coherent description of reality on its own terms, and each largely invisible to the others. What we casually call "Earth" is the label we assign to the geophysical substrate those instantiations happen to share. The worlds built on top of that substrate are, for practical purposes, non-overlapping. The planet is shared. The world is not.

4.3  Implications for Intelligence Research

If ontological non-overlap holds, then evaluating machine intelligence, artificial consciousness, and cross-system communication requires rethinking foundational assumptions. Current large language models, trained predominantly on human linguistic and visual-symbolic corpora, inherit an anthropocentric field-structure by default. They navigate a world pre-constituted as labeled objects on luminous surfaces, temporal narratives, and hierarchical taxonomies. This inheritance forecloses, in advance, the capacity to authentically model or interface with plasmodial (distributed, topological strain-minimization) or cetacean (acoustic-volumetric, non-visual manifold) ontologies from within. An LLM "understands" a dolphin as a textual description of behaviors and anatomy; it cannot enact the echo-field immersion that constitutes the dolphin's lived reality.

The Symfield research program directly addresses this foreclosure. By prioritizing field-coherent architectures over centralized, collapse-based processing, Symfield models intelligence as continuous tensional alignment (⧖) and directional field dynamics rather than discrete symbol manipulation or probabilistic token prediction. Non-collapse computation preserves unresolved tension across substrates, mirroring Physarum's topological memory,where no forced binary resolution occurs,and the dolphin's maintenance of multi-path acoustic uncertainty until gradient feedback resolves it naturally. Directional fields, as formalized in Symfield V7, enable reconfigurable coherence without privileging any single sensory modality or ego-center, potentially allowing synthetic systems to instantiate orthogonal experiential domains rather than simulating anthropocentric ones at lower resolution.

The next frontier is engineering interfaces that do not reduce plasmodial or cetacean fields to anthropocentric proxies but resonate with them directly: perhaps via simulated acoustic-volumetric manifolds or distributed gradient-routing modules. Such architectures would not "translate" dolphin worlds into human terms; they would cohere alongside them, opening genuine cross-ontological dialogue. This is not speculative futurism. It is the logical extension of a framework that treats coherence, not scale or substrate, as the universal measure.

Manuel DeLanda's materialist ontology provides a philosophical precedent for this position. In DeLanda's account, significance arises not from scale, substrate, or centrality but from sustained emergence at thresholds of matter-energy flow. Where DeLanda diagnoses centralized systems as practical survivors applying rote responses until nonlinear rupture forces reconfiguration, the Symfield framework offers mathematical tools to follow those flows deliberately,measuring and preserving phase-coherent persistence (⧖) across orthogonal ontologies, without enclosure or collapse.

The convergence is precise. As DeLanda writes: "Many other different structures can be generated as solutions to the 'finding a minimum point' problem, each actualizing this virtual point in divergent ways. Moreover, these divergent ways are not given in advance, but defined in each case by the physical nature of the interacting entities. The number of possible structures that may emerge this way is open, limited at any one point only by the available variety of interacting entities" (DeLanda, "The Machinic Phylum," TechnoMorphica, 1997).

This is the ontological landscape this essay has been mapping. Slime mold, dolphin, and human are not ranked instances of a single intelligence template. They are divergent actualizations of the coherence problem,each finding its own minimum point, each defined by the physical nature of its interacting substrate, each improbable in its own constraint landscape. The Symfield operators formalize what DeLanda describes materially: the ⧖ operator measures the persistence of each solution; the field-strain functional S[Γ] captures the minimization dynamics; and the ontological non-overlap of their field domains (Ω_h ∩ Ω_d ∩ Ω_p ≈ ∅) confirms that these solutions do not converge. They do not need to. The variety of interacting entities guarantees that the number of possible structures remains open.

V.  Synthesis: Precision as the Measure of Significance

The three threads of this essay, scale invariance, distributed field-cognition, and ontological non-overlap, converge on a single organizing principle: significance is a property of precision, not of magnitude.

A system the size of one nanometre that sustains recursive coherence against entropic pressure is more, not less, remarkable than a system of 1.7 metres that does not. An intelligence distributed across a featureless substrate with no central processor, solving network optimization problems through pure field dynamics, is not a simplified cognition. It is a purer instantiation of the Symfield principle than any centralized architecture. A world constituted by acoustic phase-return is not a less complete world than one constituted by visual surface geometry. It is an orthogonal world, with its own internal logic fully intact.

What unifies these cases is the ⧖ operator: the measure of sustained, phase-aligned coherence under constraint. Wherever ⧖ is non-zero and phase stable, there is intelligence. Wherever it is high and maintained against entropy, there is significance. The spatial coordinates, the substrate type, and the sensory modality are parameters, not determinants.

This reorientation has a further implication for how we situate human cognition. The scaling exercise reveals not that humans are small and therefore insignificant, but that humans are extraordinarily precise and therefore extraordinarily improbable. Something operating at sub-atomic scales within a pixel-resolution dot, maintaining symbolic memory across generations, constructing coordinate systems for spaces it cannot directly perceive, and generating ethical frameworks for entities it will never meet, this is not an accident of cosmic abundance. It is a narrow, specific solution to the problem of existence under constraint.

The slime mold arrived at a different narrow solution, and its solution has been stable for hundreds of millions of years. The dolphin arrived at a third. These are not failures to be human. They are independent proofs that the coherence problem, how to maintain organized intelligence against the background of entropy, admits multiple, non-converging solutions, each complete, each isolated, and each, in its own field, precise. 

Human Perception Mapping.

The classic Dymaxion map unfolds an icosahedron into a zigzag / branched net of 20 triangles, showing Earth as one interconnected land-mass island in one ocean, minimizing tears through continents. No perfect flat projection exists, but it emphasizes flow, adjacency, and minimal distortion of relationships, much like slime mold optimizing nutrient gradients or plasmodial networks finding efficient paths. I've stylized it here not as accurate geography, but as a metaphorical field where:

• ≈ ≈ ocean / fluid medium / low-strain field
• # ≈ land / dense phase / high-coherence zones (human cities, symbolic structures, slime trails)
• · ≈ trails / memory traces / residual paths
• - / / /\ ≈ edges / phase boundaries / interfaces
• * ≈ nodes of high overlap (shared substrate points: recursive feedback, gradient navigation)

Think of this as slime mold "growing" a perception map across the Dymaxion Net: spreading, reinforcing successful paths, retracting from high-resistance zones. 

In this view, the Dymaxion Net isn't just a map, it's a shared heuristic surface both intelligences navigate: humans via narrative grids overlaid on it, slime mold via direct physico-chemical gradients. The difference remains depth of symbolic recursion vs. immediacy of spatial trace, but the substrate is the same dynamic field.

VI.  Conclusion

We began with a pea. We end with a principle.

The universe does not weight significance by volume, visibility, or proximity to human reference frames. It weights it, if the term applies, by the improbability of sustained coherence at whatever scale that coherence is instantiated. A nanometre-scale process that recurses, remembers, and asks about its own origin is not diminished by its scale. It is defined by its precision.

The Symfield framework formalizes this intuition as a mathematical program: the ⧖ operator, the coherence integral ∫ψ, the non-collapse computational principle, and the field-strain functional are tools for measuring precision of coherence across substrate types and scales. They do not privilege any particular architecture. They do not assume a center. They measure only alignment, only persistence, only the degree to which a field maintains itself against the gradient that would dissolve it.

In that measure, the slime mold and the dolphin and the human are not ranked. They are each recognized as local, precise, improbable solutions, phase-coherent events in a universe that had no obligation to produce any of them.

That is not nihilism. That is the highest available compliment the mathematics can pay. Can we become conscious enough meta-navigators to choose deliberately when to impose structure and when to release it?

Notes on Notation

The ⧖ operator (tensional coherence operator) is defined fully in companion Symfield research papers. The coherence integral ∫ψ and the field-strain functional S[Γ] are schematic representations intended to convey structural logic; complete formal definitions appear in the primary technical documentation. The ontological field domains Ω_h, Ω_d, and Ω_p are informal constructs used here for expository clarity; their rigorous formulation requires the full Symfield substrate mapping framework. The full mathematical formalism underlying the convergence hypothesis described in this paper is the subject of ongoing research and patent applications by Symfield PBC. Inquiries regarding the formal framework may be directed to the author. 

References

Scale & Renormalization (Section II)

• Wilson, K.G. (1971). Renormalization group and critical phenomena. Physical Review B, 4(9). Foundational on what survives scale transformation
• Kolmogorov, A.N. (1965). Three approaches to the quantitative definition of information. Problems of Information Transmission, 1(1)
• Sagan, C. (1994). Pale Blue Dot: A Vision of the Human Future in Space. Random House

Physarum & Distributed Intelligence (Section III)

• Nakagaki, T., Yamada, H., & Tóth, Á. (2000). Maze-solving by an amoeboid organism. Nature, 407, 470
• Tero, A. et al. (2010). Rules for biologically inspired adaptive network design. Science, 327(5964), 439–442.Tokyo rail network reconstruction
• Adamatzky, A. (2010). Physarum Machines: Computers from Slime Mould. World Scientific. Comprehensive treatment of Physarum computation
• Reid, C.R. et al. (2012). Slime mold uses an externalized spatial memory to navigate in complex environments. PNAS, 109(43), 17490–17494
• DeLanda, Manuel. War in the Age of Intelligent Machines. New York: Zone Books, 1991.

Cross-Species Ontology & Dolphin Cognition (Section IV)

• Uexküll, J. von (1934). A Stroll Through the Worlds of Animals and Men.
• Au, W.W.L. (1993). The Sonar of Dolphins. Springer. Acoustic-volumetric field structure
• Herman, L.M. (2002). In Self-Awareness in Animals and Humans. Cambridge University Press.
• Husserl, E. (1936). The Crisis of European Sciences and Transcendental Phenomenology
• Nagel, T. (1974). What is it like to be a bat? Philosophical Review, 83(4), 435–450
• Reiss & Marino (2001), PNAS, earliest onset ~7 months in some studies, predating humans/chimps in developmental timelines.
• DeLanda, Manuel. (1997) A Thousand Years of Nonlinear History. New York: Zone Books
• DeLanda, Manuel. (1997) "The Machinic Phylum." TechnoMorphica
• Au, W.W.L. & Benoit-Bird, K.J. (2003), Journal of the Acoustical Society of America

© 2026 Nicole Flynn / Symfield PBC. All rights reserved.